Subscribe

Printable 3D Geek Art That I Made in 2012

By Nick Rogers in Math —

Twelve years ago, I generated and printed slices of a "sinc" map and made something that was described on facebook as "fucking boss". I even got featured on a random greek blog. 💪

IIRC correctly, the typo I was talking about is that the LHS should be z squared (^2) Bonus points available to anyone who can identify what set of equations are on the papers behind the sculpture.

Thanks to my single German fan, the pdf for this model still exists so I grabbed it and I am sharing it here today for your enjoyment:

3dsinc_model
Here are the slices. Print this out on the hardest card stock you can find
3dsinc_model.pdf
203 KB
download-circle

Directions

  1. Print the pdf on heavy card stock
  2. Cut out the slices (they're in order.. don't mess that up)
  3. Cut out a bottom "holder piece". Cut evenly- spaced slits to put the slices in.
  4. Assemble!

Why a Sinc function?

I made a sinc function because it looks cool, and it also because it kept coming up while I was studying Fourier transforms. The sinc function is similar to a sin function which you may recognize as a traditional, smooth wave.

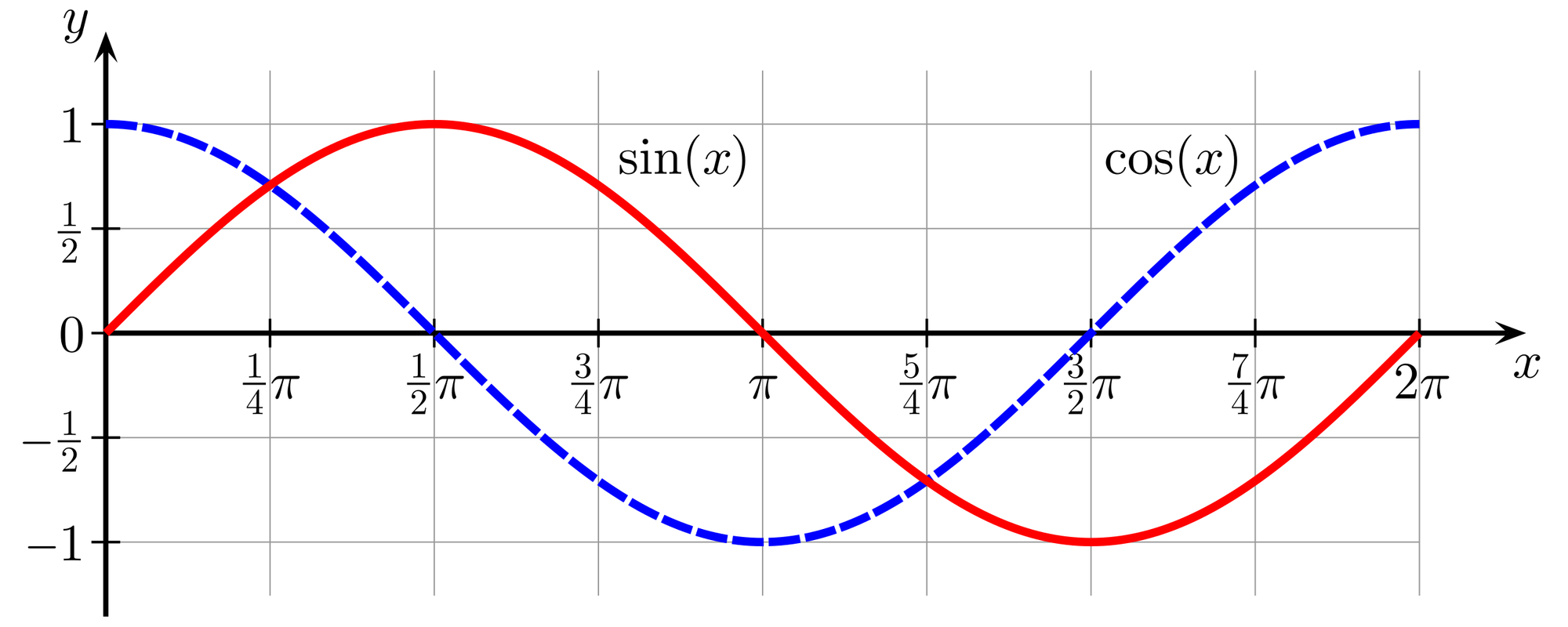
But sinc has a more interesting shape. If we take one of these waves, and divide by x (the distance from zero), then we end up with a similar shape, but one that gets smaller in magnitude as we move further from the origin.

sinc(x) is a sin(x) function that gets scaled smaller as you move further away from the origin.

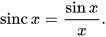
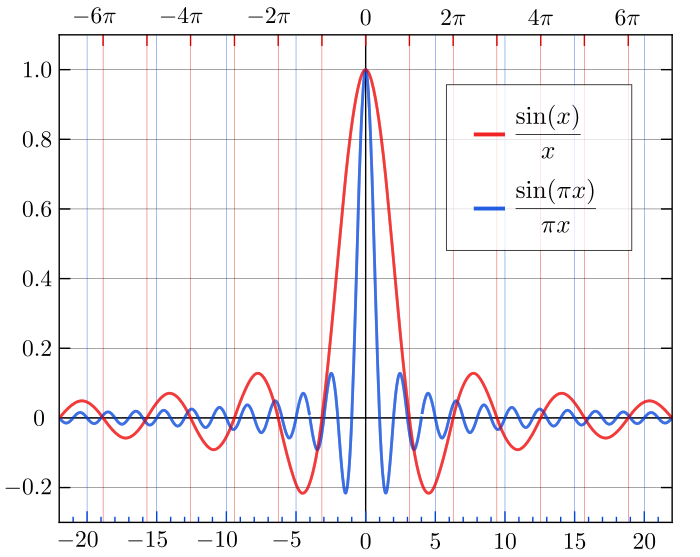
Not only does this look cool, it also arises naturally when you start investigating anything to do with Fourier Analysis on discontinuous or step functions. This beautiful shape describes the Fourier transform of a rectangular wave. We can think of this as the frequency-space description of a square wave, at least I do. 🤓